Find The Volume Of A Sphere With A Radius Of 6 Units

The volume of sphere is the capacity it has. It is the space occupied by the sphere. The volume of sphere is measured in cubic units, such as m3, cm3, in3, etc. The shape of the sphere is round and three-dimensional. It has three axes as x-axis, y-axis and z-axis which defines its shape. All the things like football and basketball are examples of the sphere which have volume.

For example, the space that a substance or 3D shape occupies or contains. Volume is often quantified numerically using the SI derived unit, the cubic metre. Volumes of some simple shapes, such as regular, straight-edged, and circular shapes can be easily calculated using arithmetic formulas. Volumes of complicated shapes can be calculated with integral calculus if a formula exists for the shape's boundary. One-dimensional figures and two-dimensional shapes are assigned zero volume in the three-dimensional space. The unit of volume of a sphere is given as the 3.

The metric units of volume are cubic meters or cubic centimeters while the USCS units of volume are, cubic inches or cubic feet. The volume of sphere depends on the radius of the sphere, hence changing it changes the volume of the sphere. There are two types of spheres, solid sphere, and hollow sphere. The volume of both types of spheres is different. We will learn in the following sections about their volumes. If you ever wondered what's the volume of the Earth, soccer ball or a helium balloon, our sphere volume calculator is here for you.

It can help to calculate the volume of the sphere, given the radius or the circumference. Also, thanks to this calculator you can determine the spherical cap volume or hemisphere volume. The purpose of this activity is to build from the concrete version in the previous activity to a generalized formula of a sphere with an unknown radius. The previous activity prepared students with strategies to work through this task where they must manipulate the variables in the volume equations. Students first calculate the volume of the cylinder and cone in the activity and use what they learned in the previous activity to calculate the volume of the sphere.

Finally, they are asked about the relationship between the volume of the cylinder and sphere, which connects back to the discussion of the previous activity. In this lesson, you'll learn how to find the volume of a sphere with a radius of 4 inches. A sphere is a 3-dimensional round object. The volume is how space is inside the sphere. When you want to find out how much space is inside such a sphere, you'll follow these steps to calculate the volume of the sphere. A sphere is the shape of a basketball, like a three-dimensional circle.

Just like a circle, the size of a sphere is determined by its radius, which is the distance from the center of the sphere to any point on its surface. The formulas for the volume and surface area of a sphere are given below. Here, we have a rectangular prism with sides that are different in distance. We have a base of 12 cm, a height of 8 cm, and a length of 6 cm.

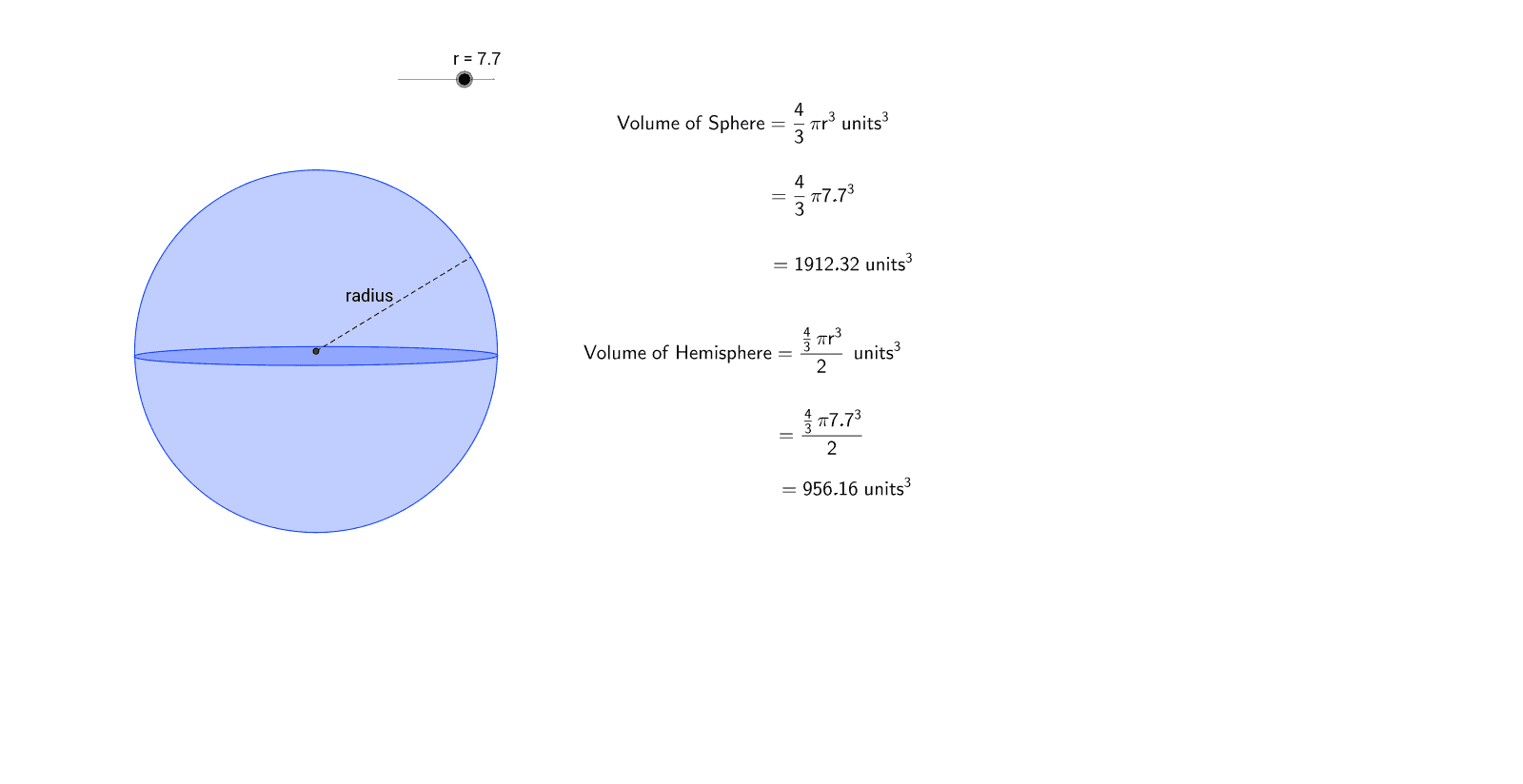
Now, all we need to do is plug those numbers into our formula, and once we solve, we get 576 cm cubed. The formula for the volume of a sphere is 4/3 times pi times the radius cubed. Cubing a number means multiplying it by itself three times, in this case, the radius times the radius times the radius. A sphere is a three-dimensional solid with no base, no edge, no face and no vertex. Sphere is a round body with all points on its surface equidistant from the center. The volume of a sphere is measured in cubic units.

The volume of a sphere is the amount of space occupied by it. For a hollow sphere like a football, the volume can be viewed as the number of cubic units required to fill up the sphere. A sphere is a three-dimensional solid with no face, no edge, no base and no vertex. It is a round body with all points on its surface equidistant from the center. This online calculator will calculate the 3 unknown values of a sphere given any 1 known variable including radius r, surface area A, volume V and circumference C. It will also give the answers for volume, surface area and circumference in terms of PI π.

A sphere is a set of points in three dimensional space that are located at an equal distance r from a given point . Now, let's look at how to calculate the volume of a triangular prism, a rectangular prism, a sphere, and a cone. This distance r is the radius of the sphere, and the given point is the center of the sphere. Show the video one more time and ask students to think about how we might calculate the volume of the sphere if we know the radius of the cone or cylinder.

Give students 1 minute of quiet think time followed by time for a partner discussion. Give students time to work on the task followed by a whole-class discussion. Then students watch a video that shows a sphere inside a cylinder set up like the image. A cone with the same base and height as the cylinder is introduced and its contents poured into the sphere, completely filling the empty space between the sphere and the cylinder.

Students are asked to record anything they notice and wonder as they watch the video and a list is created as a class. The volume of a 3 -dimensional solid is the amount of space it occupies. Be sure that all of the measurements are in the same unit before computing the volume. Find the volume of a cone by multiplying 1/3 times the area of the base times the height, or multiplying 1/3 times pi (π) times the radius squared times the height.

The sphere has a diameter of 20 meters. This is all the information we need to plug in and solve our equation. We are looking for the radius, and we know that the radius is equal to half of the diameter, which means that our radius is equal to 10 meters. When we plug 10 into our formula, and solve, we get 4,188.9 meters cubed.

Given radius of sphere, calculate the volume and surface area of sphere. In this discussion, emphasize language used to help students make sense of strategies used to calculate the volume of the sphere. These exchanges strengthen students' mathematical language use and reasoning of volume.

Ask, "In the previous lesson we thought about hemispheres in cylinders. Which is bigger, the volume of the cylinder or the volume of the sphere? Do you think the bigger one is twice as big, more than twice as big, or less than twice as big? " then give students 1 minute of quiet think time. Invite students to share their responses and keep their answers displayed for all to see throughout the lesson so that they can be referred to during the Lesson Synthesis. In this activity, students begin by looking at an image of a sphere in a cylinder.

The sphere and cylinder have the same radius and the height of the cylinder is equal to the diameter of the sphere. Students consider the image and reason about how the volumes of the two figures compare to get a closer estimate of the volume of the sphere. The volume of a sphere is four thirds pi times the radius cubed.

The total space occupied by a section of the sphere is called the volume of a section of a sphere. A section of a sphere is a portion of a sphere. The volume of a section of a sphere is expressed in square units. Let us take an example to learn how to calculate the volume of sphere using its formula. The volume of a sphere is the measurement of the space it can occupy. A sphere is a three-dimensional shape that has no edges or vertices.

In this short lesson, we will learn to find the volume of a sphere, deduce the formula of volume of a sphere and learn to apply the formulas as well. Once you understand this chapter you will learn to solve problems on the volume of the sphere. The volume V of a sphere is four-thirds times pi times the radius cubed.

Record and display student-created volume of a sphere approximation formulas for all to see. As we learned in the previous section, the volume of the spherical cap is (1/3)πh2(3R - h) or (1/6)πh(3a2 + h2). Thus, we follow the steps shown below to find the volume of the spherical cap. The formula for measuring the volume of a sphere is (4/3)πr3. We can simply measure the volume of any spherical shell by substituting the values of the parameters like radius and diameter in the volume formula. The volume of sphere formula can be given for a solid as well as the hollow sphere.

A globe of Earth is in the shape of a sphere with radius 14[/latex] centimeters. Round the answer to the nearest hundredth. Find the volume of a rectangular prism by multiplying its length times its width times its height. Assume that the volume of the sphere is made up of numerous thin circular disks which are arranged one over the other as shown in the figure given above.

The circular disks have continuously varying diameters which are placed with the centres collinearly. A thin disk has radius "r" and the thickness "dy" which is located at a distance of y from the x-axis. Thus, the volume can be written as the product of the area of the circle and its thickness dy. Write an expression to represent the volume of the sphere, in cubic units.

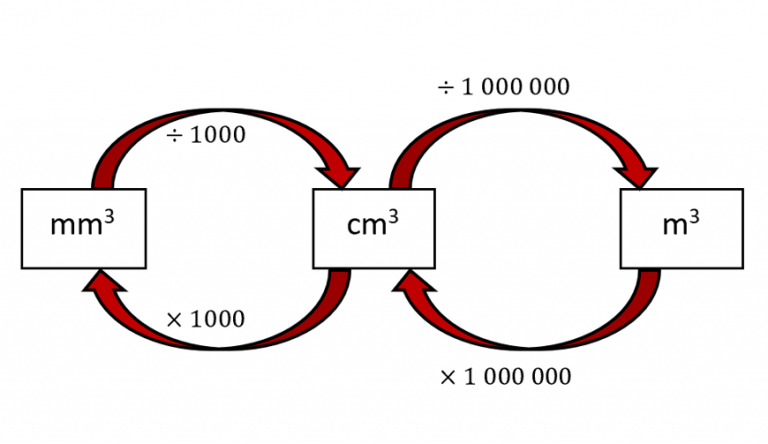
The water level in a cylindrical container of radius 0.5 m is 3.2 m. When a spherical solid object is completely submerged in the water, the water level rises by 0.6 m. The volume of a sphere is measured in cubic units, i.e., m3, cm3, in3, ft3, etc.

However, using calculus, the volume of a cone is the integral of an infinite number of infinitesimally thin circular disks of thickness dx. The calculation for the volume of a cone of height h, whose base is centered at with radius r, is as follows. Since it is already known that the volume of a sphere is 4/3 Pi radius cubed, all that is left is to replace all the variables in the formula. As we learned in the previous section, the volume of the spherical segment is (1/6)πh(3R12 + 3R22 + h2). Thus, we follow the steps shown below to find the volume of the spherical segment.

In this section, we will discuss the volume of a section of a sphere along with solved examples. Let us start with the pre-required knowledge to understand the topic, volume of a section of a sphere. The volume of a three-dimensional object is defined as the space occupied by the object in a three-dimensional space. Reviewing our data so far, this means that the radius of the sphere runs from the center, (–3,0), to the edge, .

If we find the distance between these two points, we can ascertain the length of the radius. From that, we will be able to calculate the volume of the sphere. Your browser does not support the HTML5 canvas tag.Input radius or diameter length to calculate the volume of a sphere.

The volume of any sphere is 2/3rd of the volume of any cylinder with equivalent radius and height equal to the diameter. Stay tuned with BYJU'S – The Learning App for more information on volume of the three-dimensional objects and also learn other maths-related articles. Let us see some examples of calculating the volume of spheres of different dimensions. The volume of sphere is the amount of space occupied, within the sphere. For example, suppose the volume of the sphere is 100 cubic units.

Multiplying that amount by 3 equals 300. A cylinder has a radius of 2 units and height of 5 units. Remember, if you don't write out your measurement units while you are evaluating the formula, you'll need to remember to write the measurement unit in for your answer and cube it. Read this how-to lesson to learn what steps you need to take to find the volume for a sphere with a radius of 4.

Learn what the formula is and how to use it. A ball of radius 12 has a round hole of radius 6 drilled through its center. Find the volume of the resulting solid. I tried finding the volume of the sphere and the volume of the cyclinder then subtract however that did not work.

The amount of cubic units of the volume of a sphere is double the amount of whole surface area of th... A solid metallic sphere of radius 6 cm is melted to form 27 equal small solid spheres. The radius of a solid sphere is 6 centimetres. A manifold has a volume form if and only if it is orientable. An orientable manifold has infinitely many volume forms, since multiplying a volume form by a non-vanishing function yields another volume form.

On non-orientable manifolds, one may instead define the weaker notion of a density. Integrating the volume form gives the volume of the manifold according to that form. As we learned in the previous section, the volume of the spherical sector is (2/3) πR2h. Thus, we follow the steps shown below to find the volume of the spherical sector. Showing where these formulas come from, like we did for a rectangular solid, is beyond the scope of this course. We will approximate \pi [/latex] with 3.14[/latex].

In geometric terms, a sphere is defined as a set of points that are a given distance from a given point. To calculate the volume of the full sphere, use the basic calculator. The spherical cap volume appears, as well as the radius of the sphere. They are equal to 287 cu in and 4.2 in for our example. Choose to use the diameter or radius to calculate the volume.